MATEMATICA DEGLI DEI: ASSIRI ED EGIZI (2)
Il presente articolo è stato pubblicato su Nuove Vie e riprodotto qui per gentile concessione dell’Autore.
Qui la prima parte: Matematica degli dei, i Maya (1)
I Babilonesi si impadronirono della matematica, sumera, e la portarono avanti, così come dei Sumeri presero la scrittura cuneiforme. Questo è un tipo di scrittura del tutto peculiare che ben si adattava alle risorse della Mesopotamia dove la carta era sconosciuta, anche sotto forma di papiro. Si utilizzavano invece tavolette di creta su cui venivano riportati simboli, che denotavano parole o numeri, impressi con uno speciale stilo che lasciava un’impronta nella creta morbida. La tavoletta di creta veniva poi cotta al sole e il messaggio rimaneva nella sua forma definitiva non più alterabile. Per generare tutti i numeri i Babilonesi si servivano di soli due simboli: ![]() che indicheremo per comodità con V, equivalente all’unità, e
che indicheremo per comodità con V, equivalente all’unità, e ![]() che indicheremo con <, equivalente alla decina. Per esprimere i diversi valori questi simboli venivano variamente posizionati, per cui la notazione era contemporaneamente posizionale e sessagesimale. Ed ecco una tabella con la riproduzione dei sessanta numeri del sistema babilonese.
che indicheremo con <, equivalente alla decina. Per esprimere i diversi valori questi simboli venivano variamente posizionati, per cui la notazione era contemporaneamente posizionale e sessagesimale. Ed ecco una tabella con la riproduzione dei sessanta numeri del sistema babilonese.

Vale la pena di notare che, pur essendo il sistema sessagesimale, esso deriva chiaramente da uno su base decimale, infatti i simboli, come abbiamo detto prima, rappresentano unità e decine.
I numeri vanno letti da sinistra a destra, di modo che la cifra più a destra rappresenta le unità. Stranamente i Babilonesi non avevano il concetto di zero e questo comportava una difficoltà, perché a differenza dei Maya non erano in grado di indicare una categoria vuota.
Prendiamo per esempio il numero VVV: che cosa rappresenta in realtà, VVV (3), oppure VV-V (121), V-V-V (3661), oppure V-VV (62)?
Il problema nasce proprio dal fatto di non disporre di uno zero posizionale, come quello dei Maya. Il problema è stato risolto con il sistema della spaziatura, cioè distinguendo V V da VV, o scrivendo i caratteri cuneiformi quasi incollati l’uno all’altro per indicare un unico gruppo di simboli.
I matematici babilonesi erano sotto molti aspetti piuttosto avanzati. Per esempio conoscevano le frazioni sessagesimali, analoghe alle nostre frazioni decimali. Per fare un esempio, la frazione 1/8 può essere scritta in frazioni decimali come la somma di 1/10 + 2/100 + 5/1000 = 1/8. mentre in frazioni sessagesimali diventa 7/60 + 30/3600. In questo caso il sistema sessagesimale rappresenta un vantaggio, perché 60 ha come divisore i numeri primi 2,3,5 mentre 10 ha come divisori i numeri primi 2,5. Questo comporta che col sistema sessagesimale il numero di frazioni esprimibili con frazioni sessagesimali (cioè con il denominatore di 60 o multipli di 60) è superiore a quello di frazioni esprimibili con frazioni decimali.
È interessante notare come i Babilonesi fossero anche in grado di esprimere il quadrato di un numero. Al museo del Louvre, a Parigi, è conservata una tavoletta in cui è riportato il calcolo del quadrato del numero 147, che in sessagesimale può essere espresso con la notazione 2,27, cioè 2 sessantine più 27 unità. Il calcolo effettuato sulla tavoletta dà 6,0,9 , ossia 60x60x6+9, in caratteri cuneiformi:
![]()
Appare da questa riproduzione un grosso problema, la mancanza dello zero posizionale di cui dicevamo prima. Infatti così com’è la scritta potremo anche indicare il numero 6,9, ossia 60×6+9=369. In questo particolare caso sembra che lo scriba si sia reso conto della possibilità di confusione e abbia lasciato di proposito uno spazio di separazione maggiore del solito tra i due gruppi di cifre. Ma se gli zeri da introdurre fossero stati più di uno? Per esempio per un numero del tipo 6,0,0,0,9 ?
A un certo punto, in epoca molto più tarda, anche i Babilonesi hanno risolto il problema con un segno d’interpunzione che indicasse appunto assenza di unità di un certo ordine. Tale segno di interpunzione ha avuto svariate forme; qui di seguito è riprodotta la più diffusa: ![]() quella dei due cunei inclinati, che nel testo indicheremo per semplicità con \\.
quella dei due cunei inclinati, che nel testo indicheremo per semplicità con \\.
È interessante notare che mentre il simbolo di assenza di unità di un certo ordine, che chiameremo per comodità zero, era usato dai matematici solo in posizione mediana, gli astronomi babilonesi dal 1500 a.C circa cominciarono a utilizzarlo anche in posizione terminale, dandogli quindi un valore di vero e proprio operatore, di modo che 60 poteva essere scritto come
V\\
oltre che in posizione iniziale, così da esprimere valori frazionari. Per fare un esempio, ripreso da una tavoletta, il numero 30/602 è espresso come 0+0/60+30/602, ossia in simboli
\\ \\ <<<.
Nel territorio della Mesopotamia, le lingue predominanti furono l’assiro e l’accadico, ecco i nomi dei numeri in queste due lingue: 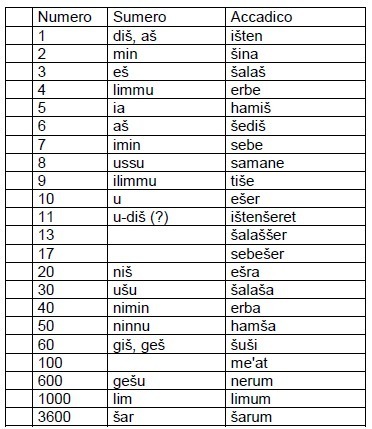
LA CIVILTÀ EGIZIA
Abbiamo lasciato di proposito la civiltà Egizia per ultima, perché quando si guarda alle conquiste del mondo antico si finisce sempre per arrivare alla terra dei faraoni, quasi che questa fosse stata depositaria di segrete conoscenze che poi si sono diffuse ad altre civiltà. E anche nel campo della matematica le tracce egiziane sono facilmente individuabili in civiltà minori, a volte geograficamente molto distanti, come le civiltà cretese, ittita, elamita e azteca. Ma è giusto parlare di tracce egizie in queste civiltà, o più semplicemente queste civiltà e quella egizia hanno attinto le loro conoscenze da una civiltà precedente e per questo presentano fortissime somiglianze?
La scrittura geroglifica egiziana risale all’inizio del Vecchio Regno, 3000 a.C. circa, ed è appunto in questo periodo che furono costruite le prime piramidi, opere grandiose che dimostrano conoscenze ingegneristiche di livello superiore e quindi conoscenze matematiche elevate. Eppure, stranamente, la matematica egizia è molto semplice, elementare, con sprazzi di intuizioni geniali.
Sembra un controsenso, ma tutto appare più chiaro se si considera la casta sacerdotale egizia, una casta totalmente chiusa, che delle proprie conoscenze facevano un mistero con connotazioni soprannaturali. E allora, la matematica egizia di cui ci sono arrivati documenti, è proprio tutta la matematica? O i sacerdoti avevano conoscenze molto più approfondite? E in tal caso da dove venivano queste conoscenze?
Oggi ciò che sappiamo della matematica egizia deriva da iscrizioni su monumenti e templi, che per forza di cose non potevano andare oltre a semplici enumerazioni di nemici catturati o uccisi, oggetti posseduti o date di rilevante importanza.
Probabilmente esistevano anche documenti più propriamente matematici, ma essendo questi su papiro sono andati facilmente distrutti a causa della deteriorabilità del materiale. Due documenti però sono arrivati fino a noi e sono di rilevante importanza; si tratta del Papiro di Rhind e del Papiro di Mosca.
Il primo, qui sotto riprodotto, prende il nome dall’egittologo scozzese Henry Rhind che l’acquistò a Luxor nel 1858. Si tratta di un rotolo di grandi dimensioni (è lungo ben 6 metri e largo 35 centimetri) e stando a quanto afferma il suo compilatore, lo scriba Ahmes (1650 a.C.), sarebbe la copia di un documento di 200 anni prima.

Il Papiro di Rhind contiene 87 problemi di vario genere, soprattutto pratico. I primi sei problemi riguardano la divisione di alcune pagnotte tra dieci persone. Ci sono poi problemi che riguardano le frazioni e altri che chiedono la soluzione di un’equazione, altri ancora sono di tipo geometrico. Per esempio il problema 26 chiede: Aggiungendo una quantità a un quarto della stessa quantità si ottiene 15. Qual è questa quantità?
In termini moderni si tratta di un’equazione di primo grado espressa dalla formula x+1/4 x = 15 , dove x è la quantità incognita da trovare. Un problema molto semplice da scuola media. Ma per gli antichi egizi che avevano a che fare con un sistema numerico piuttosto scomodo da usare, la soluzione non era così facile.
Il Papiro di Mosca è così chiamato perché custodito nel Museo delle Belle Arti di Mosca ed è della stessa epoca di quello di Rhind. È ignoto però il nome dello scriba che lo compilò. I problemi contenuti sono 25, alcuni dei quali geometrici.

Ma vediamo ora come sono rappresentati i numeri nella scrittura geroglifica. Innanzi tutto occorre premettere che la scrittura egizia, che è essenzialmente pittorica, può essere letta da sinistra a destra o da destra a sinistra, e, se in verticale, dall’alto in basso. Il senso della lettura è però sempre chiaramente indicato, in quanto i simboli possono essere scritti in due forme, rivolti a sinistra o rivolti a destra. Qui di seguito è riportato un esempio di lettura da destra a sinistra (simboli rivolti a sinistra):

Non è ben chiaro perché gli Egizi abbiano scelto una doppia chiave di lettura, ma è probabile che, al pari degli Aztechi o dei Maya, dessero una grande rilevanza all’apparenza grafica della scrittura, insomma non avrebbero cercato tanto il facile quanto il bello.
Anche i numeri seguono questa chiave di lettura per cui esiste una doppia serie di numeri, ognuna delle quali viene utilizzata a seconda del senso della lettura del testo corrente.
Il sistema di numerazione egizio, risalente all’inizio del terzo millennio a.C., è a base decimale e non è di tipo posizionale. I numeri sono espressi per potenze di dieci, così l’unità è indicata da un trattino verticale, la decina da un archetto rovesciato, il centinaio da una spirale, il migliaio da un fiore di loto, la decina di migliaia da un dito alzato leggermente inclinato a secondo della direzione della lettura, il centinaio di migliaia da una specie di girino caudato e il milione da un uomo con le braccia levate al cielo. I simboli naturalmente seguono sempre l’orientamento della lettura. Nel caso si debbano esprimere più unità di un certo grado, il simbolo viene ripetuto tante volte quanto è necessario.
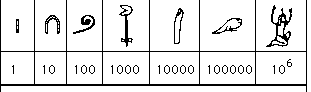
Il sistema non è molto pratico e i calcoli diventano spesso difficoltosi, un po’ come succederà coi numeri romani. Per scrivere un certo numero si parte dalle unità di ordine superiore e si prosegue man mano con quelle di ordine inferiore. Non esiste lo zero, ma in realtà non ce n’è bisogno in quanto ogni ordine ha un suo determinato simbolo, quindi non c’è possibilità di confusione. Se al simbolo della decina segue quello del migliaio, vuole semplicemente dire che non ci sono centinaia. Per evitare che i numeri diventassero troppo lunghi, e diventassero anche scomodi da scolpire per esempio su una stele, spesso venivano raggruppati in ordine discendente.
Un esempio in questo senso è dato dalla colonna centrale degli annali di Tutmosi III (1490-1436), i cui numeri sono così raggruppati:

ma naturalmente la fantasia degli scribi era libera di esprimersi secondo l’inventiva dell’autore.
Gli egizi conoscevano anche la frazioni, però solo quelle con numeratore uno e qualsiasi altro valore frazionario veniva espresso come somma di frazioni con numeratore uno. Facevano eccezioni solo le frazioni 2/3 e ¾ , che però non venivano usate nelle sommatorie di frazioni con denominatore uno. Anzi, in una sommatoria non veniva mai ripetuta la stessa frazione, ma si cercava un’altra combinazione. La ragione è ignota.
Così la nostra frazione 4/7 era espressa come la somma: 1/2+ 1/14
mentre 4/5 era espressa come la somma: 1/2 + 1/4 + 1/20
Le frazioni erano indicate mettendo il geroglifico della bocca in alto e sotto il numero che esprimeva il denominatore. Come negli esempi qui sotto riportati:
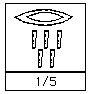
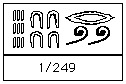
Le frazioni ¼, ½, 2/3 e ¾ invece erano rappresentate con simboli a se stanti, rispettivamente: 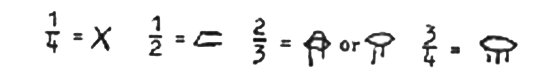 Infine esisteva anche un’altra scrittura dei numeri, quella ieratica, che aveva il vantaggio di essere più compatta e quindi di richiedere meno simboli per esprimere un numero, ma che di converso richiedeva la memorizzazione di un maggior numero di simboli, come si può vedere dalla sottostante tabella:
Infine esisteva anche un’altra scrittura dei numeri, quella ieratica, che aveva il vantaggio di essere più compatta e quindi di richiedere meno simboli per esprimere un numero, ma che di converso richiedeva la memorizzazione di un maggior numero di simboli, come si può vedere dalla sottostante tabella:
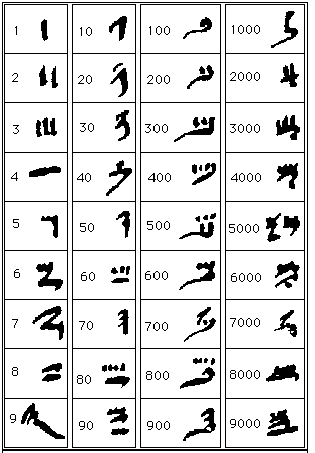
Con la numerazione ieratica, che non è posizionale, i simboli possono essere posizionati sia in ordine crescente che decrescente.
Il sistema ieratico e quello geroglifico hanno convissuto per circa 2000 anni, il primo era utilizzato preferibilmente per la scrittura su papiro e il secondo per la scrittura mediante incisione su pietra.
Gli egizi conoscevano bene l’addizione e la sottrazione, ma riuscivano anche a fare operazioni di moltiplicazione e divisione, ricorrendo a forme iterative di addizioni e sottrazioni. Vediamo un esempio di moltiplicazione, come è riportato nel Papiro di Rhind:
Si vuole moltiplicare 41 per 59 e lo scriba Ames così procede: prende 59 e lo somma a se stesso, poi prende il risultato ottenuto e lo somma di nuovo a se stesso e così continua
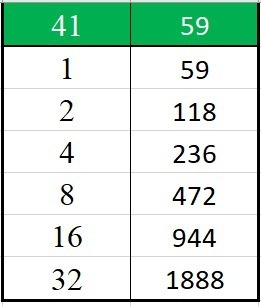
A questo punto poiché 64 > 41, il procedimento si arresta, e si procede invece con una serie di sottrazioni:
41 – 32 = 9, 9 – 8 = 1, 1 – 1 = 0
da cui risulta 41 = 32 + 8 + 1.
Segniamo con un asterisco i numeri di destra corrispondenti a questi ultimi tre numeri e sommiamoli tra loro.
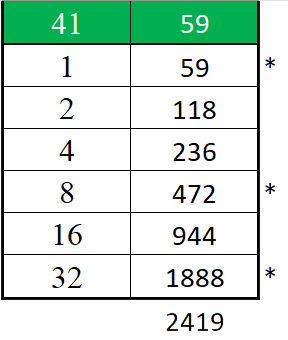
Ed ecco che la moltiplicazione è stata ottenuta solo con addizioni. In realtà che cosa si è ottenuto con questo sistema? Si è scomposto il numero 41 in una somma del tipo 32+8+1 e ognuno di questi numeri è stato moltiplicato per 59 (facendone ripetutamente la somma come nella prima figura), per cui in notazione moderna, si può scrivere
1×59+8×59+32×59 = 2.419.
Visto che il sistema funziona sempre con qualsiasi numero, gli Egizi se ne sono serviti tranquillamente e anche per la divisione sono ricorsi a un sistema analogo, che qui non riportiamo.
Pur disponendo di questi meccanismi matematici piuttosto semplici, gli antichi egizi erano però riusciti a calcolare il valore di pi greco con buona approssimazione. Nel Papiro di Rhind il valore è calcolato secondo questa formula (in termini moderni): 4(8/9)2 che dà 3,16. È interessante notare che il valore di pi greco compare come costante nella costruzione della Piramide di Cheope, a Giza. Infatti la cotagente dell’angolo formato dalla base della piramide con il triangolo inclinato di una faccia, angolo che è uguale a 51°50’35’’, è pari a ¼ di pi greco, mentre la secante di questo stesso angolo dà all’incirca il valore della sezione aurea (1,618034).
Le “coincidenze” matematiche della Grande Piramide non terminano però qui. L’altezza della piramide di Cheope è di 147,8 metri (altezza che è stata ricostruita in base alla struttura della piramide, visto che la sommità è andata distrutta nel tempo) e questo valore moltiplicato per un miliardo è uguale alla distanza della terra dal sole, con uno scarto minimo dell’1%. Ma la stessa unità di misura egiziana, il cubito, ha una interessante peculiarità, infatti è pari a un decimilionesimo del raggio della terra, con uno scarto di un solo centesimo di millimetro, una precisione superiore a quella del nostro stesso metro!
E allora, di nuovo, com’è possibile che con la loro rozza matematica gli Egizi siano riusciti a erigere costruzioni che presentano rapporti matematici, chiaramente non casuali, così precisi? Il sospetto che la classe sacerdotale fosse in possesso di conoscenze ben più elevate in campo matematico, e non solo matematico, non fa che rafforzarsi. Ma queste conoscenze matematiche da dove venivano? Erano il prodotto di un lento sviluppo interno nell’arco di secoli, o millenni? Oppure era un qualcosa trasmesso loro da altri, conoscenze custodite nel massimo segreto e tramandato solo all’interno della loro cerchia? E qual è il filo sottile che lega i sistemi matematici di civiltà come quella egizia, babilonese, maya, ma anche azteca, elamita, ittita, cretese, o addirittura quella cinese, civiltà in alcuni casi geograficamente molto distanti e per quell’epoca prive di contatti culturali?
Potrebbe darsi allora che questo filo sottile ci riconduca alla fine a un’unica civiltà molto più avanzata, che quando è stata distrutta ha lasciato la sua orma impressa nelle culture delle civiltà superstiti? In questo modo si spiegherebbero sia le somiglianze tra le diverse culture matematiche, sia la conoscenza di principi di ordine superiore quali la sezione aurea (phi) o il pi greco.
Se così stanno le cose, e c’è chi ne è fermamente convinto, questa civiltà non può essere che la mitica Atlantide di cui parla Platone. Quell’Atlantide avanzata scientificamente in ogni campo che non si è rassegnata a morire, ma che ha saputo trasmettere alle civiltà coeve alcuni principi di base, che sono stati a lungo sfruttati, per essere poi dimenticati, sia perché non del tutto compresi sia perché custoditi all’interno di ristrette cerchie di privilegiati e quindi destinati a morire a poco a poco, essendo venuta a mancare la linfa vitale di ogni scienza, la comunicazione e la diffusione con l’esterno, che servono ad alimentare e a fare progredire ogni conoscenza.
È interessante notare come sia nella civiltà Maya sia in quella Egizia i numeri abbiano anche un valore esoterico, che va al di là del loro significato matematico.
Ecco brevemente un quadro riassuntivo.
Maya
- Chiamato Hun. Rappresenta il concetto di “unico” presente nel mito della creazione. il Dio Unico chiamato Hunab Ku
- Il principio della dualità, fondamentale nella religione maya.
- Indicava la divisione verticale dell’universo: Terra, Inframondo, Mondo superiore.
- È il numero sacro della quadripartizione dell’universo. Ripetutamente presente nella cultura religiosa.
- È il numero della “Quinta Creazione”, quella in cui vivevano i Maya.
- Il suo valore stava nell’essere multiplo di 2 e di 3.
- Numero di grande valore esoterico, ripetutamente presente nella cultura religiosa.
- Il suo valore stava nell’essere multiplo di 2 e 4.
- Nove sono i numi tutelari dei nove strati in cui è diviso il mondo inferiore.
- Il suo valore stava nell’essere multiplo di 2 e di 5.
- Legato soprattutto al Katun 11 (il Katun è un ciclo di 20 anni, base del calendario Maya).
- Importante come multiplo di 3 e 4.
- Come per altri popoli era il “numero magico”.
- Importante come multiplo di 7.
- Importante come multiplo di 3 e di 5.
- Importante come multiplo di 4 (a sua volta importante nella cosmogonia Maya). Il 16 compare spesso nelle misure degli edifici sacri. E 16 sono stati i re della dinastia di Copán.
- Non era considerato molto importante.
- Questo numero era importante nel Calendario solare, composto di 18 periodi di 20 giorni.
- Non molto importante. Indicava anche un periodo supplementare di 5 giorni (infausti), costituente in pratica una specie di diciannovesimo periodo del Calendario civile, che serviva a fare tornare il conto dei giorni solari.
- Numero fondamentale della matematica Maya, che è a base vigesimale. Fondamentale anche per il computo del calendario Maya (cicli di 20 anni chiamati Katun e di 400 anni chiamati Baktun).
0 Non rappresenta il nulla come nella nostra civiltà, ma il completamento della serie nel Computo Lungo del calendario. Aveva anche valore di operatore matematico, per moltiplicare le unità delle cifre.
Egizi
- Rappresenta l’unità vivente dell’universo, l’Assoluto.
- La Scissione Primordiale, il mistero assoluto. Esprime la polarizzazione presente nella natura. Il conflitto eterno tra Seth e Horus.
- Rappresenta la terza forza, l’equilibrio tra forze negative e positive.
- I quattro elementi fondamentali: Fuoco, Terra, Aria, Acqua.
- Il cinque rappresenta la vitalità dell’universo. Il numero del pentagono che è in stretta connessione con la Sezione aurea.
- È il numero del tempo e dello spazio. Il numero della figura perfetta, il cubo.
- Simboleggia l’unione dello spirito con la materia. Il sette è il numero della piramide, quattro lati di base e facce triangolari.
- È l’ottavo segno zodiacale, lo Scorpione. Esprime la morte, il sesso e il rinnovamento, come nel mistero di Ermopoli: “Io sono l’Uno, che diventa Due, che diventa Quattro, che diventa Otto e poi torno Uno.”
- È il numero della Grande Enneade (gruppo di nove) l’insieme delle nove divinità che presiede alla generazione del mondo: Atum, Shu e Tefnut, Geb e Nut, Iside, Osiride, Seth e Neftis.
Antonio Bellomi
Nato nel 1945, laureato in matematica. Ha cominciato a scrivere professionalmente nel 1965, pubblicando sulla rivista COSMO. Nel 1967 il suo primo romanzo, “L’Ultimo Domani.” Dal personaggio a fumetti Martin Mystere di Alfredo Castelli, ha scritto una serie di racconti. Nel 1991 ha pubblicato “L’Impero dei Mizar” per l’editore Solfanelli, una delle più belle space-opera italiane, secondo i critici. È stato curatore di moltissime riviste di fantascienza, scoprendo vari talenti.